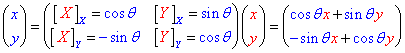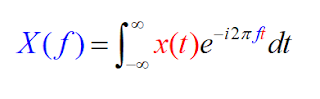Joseph Fourier y la muerte (III)

Llega ya por fin el momento de resolver el engima de la vida y de la muerte, mediante el conocimiento matemático y, en particular, atendiendo a las transformaciones de Fourier, cuyo mecanismo explicaba en el post anterior.

Recordemos la esencia del razonamiento: hay alguien que mide una cosa desde una perspectiva; otro quiere traducir esa medición a su propio lenguaje; como lo de medir pasa por creerse el centro del universo (mido desde el punto 0, mis unidades valen 1, mi plano no tiene inclinación alguna...), el truco para traducir consiste en ponerle al otro aquello que él o ella cree no padecer pero sufre desde nuestra perspectiva (que está desplazado, que sus unidades están contraídas, o que su plano está inclinado en dterminada medida...). Con todo lo cual no se pretende, evidentemente, tener razón, sino adoptar la perspectiva que, ante cada problema, resulte más conveniente, porque facilita la solución. Solución que normalmente se traduce en añadir una fuerza por aquí, o una pizca de intensidad por allá, para lograr el resultado deseado.

Curiosamente, cuando llega el momento de aplicar esto a las perspectivas tiempo y frecuencia, choca uno con la oposición de los matemáticos. En jerga de álgebra lineal, a la "perspectiva", si consiste en unos ejes de coordenadas, se le llama "base". Pero me dicen los expertos que, al menos cuando elige uno supuestas bases con infinitos componentes, en un intervalo que va desde el menos infinto al más infinito, no estamos en puridad ante tal cosa ("bases"), sino ante "espacios vectoriales". Lo he intentado aquí y hemos estado cerca, mas no ha quedado resuelto el porqué de esta technicality. Pero lo que para mí no ofrece duda es que se trata de eso, de un matiz técnico a clarificar, que no empaña para nada la maravillosa metáfora que tenemos entre manos. Máxime cuando, como digo, sirve para resolver el sentido de la vida...

La cosa va así. Si yo tomo, por ejemplo, el intervalo de mi vida entre nacimiento y muerte, puedo contar hacia adelante o hacia atrás, pero ojo: en el bien entendido de que cuando cuento hacia atrás no recorro el mismo camino en dirección contraria, sino que me paso a la otra cara de la moneda y regreso por ella. Si cuento hacia adelante, a cada instante le pongo números progresivamente más altos. Si cuento hacia atrás, el número más bajo coincide con el conjunto de mi vida. Es el período más largo. Pero puedo considerar un período que sea la mitad de largo, pero que se repite más veces, en concreto dos, dos veces por vida. O tres o cuatro o mil veces por vida. Voy así subiendo de frecuencia y digo que lo hago por el reverso de la moneda, porque ahora no la estoy llenando a base de colocar "secuencialmente" una cosa delante de la anterior, sino que adopto un enfoque "holístico" en el que las cosas ocupan todo el intervalo y las coloco una encima de la otra. En efecto, bajo esta perspectiva, la vida es una suma de patrones que la atraviesan de cabo a rabo, desde los de frecuencia más baja (período más largo) a los de la más alta (período corto). 

De esta forma, a la hora de cambiar el resultado del experimento, el experimentador tiene dos opciones. Bien cambiar lo que sucede en un instante, dándole más o menos intensidad, o bien cambiar también la intensidad, pero de una frecuencia. Un mismo resultado podría conseguirse de una u otra forma. Por ejemplo, yo podría modificar un instante tocando muchísimas, muchísimas frecuencias. O cambiar los patrones que gobiernan mi vida a base de alterar infinitos instantes. Lo lógico, sin embargo, es utilizar en cada caso el método adecuado, como decía, a la vista del objetivo perseguido.

¿Resuelve entonces esto la congoja de ver cómo la vida es frágil y fugaz? ¿Nos consuela cuando se marchan o peligran los nuestros? ¿Nos reconforta al ver que se nos escapa el tiempo de entre las manos, sin estar protagonizando la película que deseábamos? Evidentemente, no. Las observaciones que estoy haciendo le resultarían útiles al que, en su caso, estuviera haciendo el experimento de nuestras vidas y lo contemplara en su integridad o siquiera en un intervalo determinado, pero que incluye un trozo de futuro, ya esté este escrito o no, ya se pueda predecir de modo determinista o al menos probabilista. Ahora bien, yo soy el objeto de este experimento, no el experimentador. Yo estoy dentro de un pozo y no tengo esa amplitud de miras.

El mensaje, sin embargo, no tiene que ser desesperanzador ni de resignación pasiva. Bien mirado, coincide un poco con lo que dicen los expertos sobre cómo se ha de vivir. Lo único que tenemos nosotros es cada instante y lo que toca es honrarlos, a medida que llegan. Y podemos también albergar tal vez la esperanza de sintonizar con unas frecuencias que nos sirvan de guía y cambien el guión de la película, si bien esto está más allá del alcance de la mente racional, tanto por ausencia de perspectiva, como por la propia falta de capacidad de proceso. En efecto, los científicos que usan en su trabajo las transformaciones de Fourier se sirven de complejos algoritmos de cálculo, que manejan las computadoras. Si yo soy el personaje del film y quiero influir sobre el desenlace, lo más que puedo hacer es de alguna manera trasladar mi problema al guionista y ponerlo en sus avezadas manos. 

En este momento, es importante no ponerse tonto. No empezar a lloriquear, como puede estar haciendo mi propia mente, con lo de: "¿pero, oiga, quién le ha dicho a usted que hay guionista, si no lo hay, eso es una superchería; o si lo hay, cómo lo sabemos, y cómo es que pasan cosas tan malas, será un mal guionista...?" Todas esas voces son las del Enemigo, esto es, los aguafiestas. Aquí, como venía sosteniendo en otros posts, no se trata de que las cosas sean verdad, sino de si estamos ante un relato (un mito, si se quiere) que merece funcionar y puede de hecho hacerlo. Y éste, según los que saben, debe y puede funcionar. Así que esto es lo que hay que visualizar: hay que pedirle al padre Fourier que nos guíe, que juegue como un gran Niño con su computadora de última generación y monte una linda comedia que le haga reír, que sirva a sus grandes fines, mientras nosotros tambien disfrutamos al representarla.

(Y a ver si me aplico el cuento y estoy de mejor humor, pues llevo una semana de muy malas pulgas, que han padecido los empleados de las Grandes Compañías. Pobres, pienso ahora, sobre todo el de ING, que se llevó la peor parte. Perdón, amigo. Padre Fourier, pongo en general en tus manos mi relación con las multinacionales y sus servidores. Colócame en las frecuencias adecuadas: para que ellos, con sus interminables letanías y sus dejes burocráticos, no me aparten de mi camino, y para que yo no sea en sus oídos voz iracunda, sino útil y esclarecedora. Amén.)

Joseph Fourier y la muerte (II)

 

Retomando el tema que dejé apuntado en la entrega anterior, a continuación paso a explicar por qué están conectadas las transformaciones de Fourier con la muerte. Como siempre, intentaré ser ameno en la parte matemática y animo a digerirla, porque el final que reservo (la conexión entre los binomios vida-muerte y tiempo-frecuencia) es en verdad impactante.

Partimos de un problema práctico, como la distancia hasta un gato. Desde mi posición, mido que el gato está a x = 10 m. Mi hermana se halla en un punto intermedio. Ella podría hacer su propia medición, pero preferimos adivinarla por lógica, “transformando” el valor que yo he medido. En concreto, mi hermana razona así: Javier sitúa el origen de su cinta de medir (el punto 0) en su propia posición, pero yo lo coloco en la mía y para mí él se encuentra a una distancia d = -5 m; por tanto, debo añadir a sus valores lo que él, desde su posición, juzga no tener, pero desde la mía sí tiene. O sea, x = x + d = 10 + (-5) = 5 m. 

(Ya sé que a ustedes les resultaría más comprensible que mi dilecta hermana razonara así: Javier, que está más lejos, cuenta 5 m de más, que yo debo restar; y si fuera al revés, si yo estuviera entre mi hermana y el gato: Javier, que está más cerca, cuenta 5 m de menos, que yo debo añadir. Pero, señores y señores, hay que encontrar una expresión común a ambas hipótesis y esa es la que he propuesto: Javier, desde mi posición, tiene lo que sea -positivo o negativo-, pero no lo computa, pues él cree que no lo tiene; por eso, para traducir sus valores a mi posición, yo tengo que "añadir" a los suyos esa posición que a mi juicio les falta -lo cual se traducirá en suma o resta, respectivamente-.) 

Alternativamente, yo podía haber medido la posición de mi hermana (d = +5). ¡Pero cuidado! Esto me valdría para transformar sus valores a mi lenguaje. Pero, si lo que pretendo es “ponerme en su piel”, debo darle la vuelta a mi medición, cambiándole el signo, lo que nos lleva a la misma regla de transformación: - d = - (+5) = -5 = d. Por cierto, puedo comprobar que el cambio de signo funciona porque, si sumo las dos reglas, la de ida y la de venida, vuelvo al punto de partida: d + d = 0.

Para aplicar esta idea a otras situaciones, debemos generalizarla. En lugar de “posición”, hablemos de “perspectiva”. “Medir la posición del otro” será por tanto “medir dónde queda la la perspectiva del otro desde la mía”. A esto le llamo, abreviando, “medir el cambio de perspectiva”. Y en lugar de “añadir” ese cambio al valor ajeno, podemos hablar de “aplicarlo”, lo que se traducirá en la operación aritmética que corresponda. De igual modo, si soy yo el que mide la diferencia de perspectiva, ya no le “cambiaremos el signo” sino que la “invertiremos”, de la forma que proceda: haremos lo necesario para que, “aplicando” a una regla su inversa, el resultado sea siempre “no hacer nada, dejar las cosas como estaban”.

Podríamos directamente emplear esta formulación abstracta para entender la transformación de Fourier, pero quedará más claro si pasamos por otros dos ejemplos intermedios.

El primero es el que podríamos llamar multiplicativo, en vez de aditivo. Supongamos ahora que mi hermana y yo compartimos el mismo origen, pero medimos con distintas unidades. Las mías son de 1 m, mientras que las suyas miden el doble, 2m. Ahora pues la perspectiva es el tamaño de nuestras respectivas unidades. Por tanto, cuando mi hermana mide el cambio entre tales perspectivas, lo que hace es comprobar que las mías son la mitad de grandes que las suyas, esto es, que la ratio entre ellas es ½ (r = ½). Aplicar esta regla a mi valor supone, mutatis mutandis, ya no sumar, sino multiplicar: x = x * r = 10 * ½ = 5. Si hubiera medido yo esa diferencia de perspectiva, habría obtenido r = 2, pero -para ponerme en los zapatos de mi hermana- comprendería que debo invertir la regla; en este caso, como la regla es multiplicativa, al invertirla la convierto en división: r = 1/r =  ½. Y, para comprobar que hemos invertido bien, lo que hacemos es multiplicar una regla por otra (r * r =  ½ * 2), de forma que el resultado no es ya 0 (que significa no sumar) sino 1 (que significa no multiplicar), pero está bien, pues de eso se trata, de quedarnos donde estábamos.

El siguiente paso consiste en hacer el caso multidimensional. Por ejemplo, imaginemos que el gato se ha subido a un árbol. En este caso, como no tengo una escalera que me lleve hasta el animal, utilizo dos pistas: mido mi distancia hasta el pie del árbol (x) y luego proyecto una línea perpendicular desde ese punto hasta el gato (y), componiendo así un triángulo rectángulo cuya base es x y cuya altura es y, lo cual me permite calcular la distancia a recorrer, mediante el Teorema de Pitágoras, como s = √(x² + y²). Por su parte, mi hermana comparte de nuevo mi origen, pero tiene otros ejes: ella se sirve de un terraplén que se eleva hacia el gato (digamos con un ángulo θ respecto del suelo), pero no lo alcanza, por lo que tiene que completar desde cierto punto (x) con un palo que se eleva en perpendicular desde el terraplén hasta el felino (y). Ella podría entonces medir directamente su x y su y, pero como siempre preferimos transformar mis valores.

Para ello, mi hermana debe medir la diferencia entre nuestras respectivas perspectivas, lo cual ahora se traduce en cuán inclinados están mis “metros” (a los que llamaré X e Y, con mayúscula) respecto de los suyos (que denomino también con mayúscula, X e Y). Este es un juicio que se hace por dimensiones. En efecto, lo de creerse uno el ombligo del mundo y el que tiene la rectitud es una tendencia tan fuerte que hasta la sufre cada una de nuestras personalidades.

El primer paso al frente lo da la cara X de mi hermana, que desea obtener la coordenada x. Lo primero que hace esta señora es medir mis dos perspectivas: observar las proyecciones de mis metros X e Y sobre ese eje X; obtiene así unas sombras, que están acortadas, las coordenadas cos θ y -sen θ.

Toca ahora aplicar esta regla a mis valores de la distancia hasta el gato, x e y. La dama X lo hace multiplicando cada oveja por su pareja (mi valor x lo multiplica por la forma en que ella lo ve, esto es, pasándolo por la lente que es cos θ; a mi y le aplica también el corrector correspondiente, que es  -sen θ) y luego suma esos productos. Como unos son positivos y otros negativos, el resultado es el efecto neto, que viene a ser la coordenada x, esto es, cuánto tiene la distancia hasta el gato de su eje X (el terraplén).

Para obtener la coordenada y, la faceta Y de mi hermana efectúa la misma operación: proyectar mis metros X e Y sobre su eje Y y obtener la diferencia de perspectiva con Y, esto es, las ratios sen θ y cos θ, y las emplea de la misma manera.

(Todo esto funciona así gracias, a que -tanto para mí como para mi hermana- los ejes y los metros X e Y son de valor unitario y perpendiculares entre sí, pero se hace algo largo de explicar y no quiero que los árboles no dejen ver el bosque.)

En conjunto, matemáticamente, esto se presenta como un producto entre matrices: a la derecha he puesto mis valores x e y para la distancia hasta el gato, que es lo que hay que transformar, como una matriz con una columna; a la izquierda vemos otra matriz (que llamo M) con dos columnas, una para mi unidad o perspectiva X y otra para la Y, pero medidas desde la perspectiva de mi hermana, por lo que me refiero a ellas con sus respectivos nombres (X e Y), aunque indicando en subíndice qué faceta de mi hermana las mide (X o Y). La gracia de multiplicar matrices es que se hace de la forma que avanzaba antes: la columna por cada línea (cada oveja con su pareja y sumando productos), lo cual permite pasar el vector de la derecha por el filtro de las perspectivas X e Y sucesivamente, como se ve aquí: 

Pero no hay que dejarse deslumbrar por el aparato técnico. Al fin y al cabo, estamos ante lo de siempre: se coge mi medición sobre la distancia hasta el gato y se le aplica lo que le falta para valer desde la perspectiva de mi hermana. Antes eso se traducía en añadir la distancia d, luego en aplicar la ratio r y ahora en multiplicar por la matriz M, pero nada más.

Para rematar, señalo que si yo hubiera medido la perspectiva de mi hermana, habría obtenido el mismo resultado que ella, pero organizado de otra forma. En concreto, habría obtenido una matriz con los mismos senos y cosenos del ángulo que nos separa, si bien mis columnas serían sus filas. Esto me valdría para transformar hacia mi perspectiva, pero si quiero “ponerme en su piel”, debería invertir esa matriz, lo que se consigue transponiéndola, esto es, cambiando las filas por columnas. La prueba de que esto es correcto es que si multiplico una matriz de transformación por la inversa el resultado es la matriz identidad, esto es, la que deja las cosas como están (la que si se aplica, no hace nada).

Llegamos así a la transformación de Fourier, cuyo aspecto aterrador era este:

Pero es fácil descubrir enseguida a nuestros viejos amigos, con un disfraz adaptado a las nuevas circunstancias. La principal novedad es que el problema a resolver es otro: nos encontramos ahora ante una señal que oscila alrededor de un punto de equilibrio (digamos por ejemplo el maullido del gato, que consiste en compresiones y estiramientos del aire con mayor o menor amplitud). Lo cómodo sería que este sonido tuviera un período que se repite, pero si no lo tiene, nos imaginamos que lo acaba teniendo en el límite, considerando un intervalo entre el menos infinito y el más infinito.

A la hora de medir la señal yo tomo la perspectiva de los instantes temporales: mido (con un osciloscopio) la amplitud del sonido en cada momento y lo represento como una función que toma como input cada instante y da como output una magnitud una amplitud del sonido. Esto es el f(x) que se ve en la ecuación y que se corresponde con el x de la distancia hasta el gato, en los dos primeros ejemplos, o el x e y del tercero; lo único que cambia es que ahora tengo una serie continua e infinita de valores, en vez de uno o dos.

Mi hermana toma por su parte la perspectiva de las frecuencias. Y es que en efecto cualquier sonido se puede ver como una suma de oscilaciones a distintas frecuencias, cada una con su amplitud correspondiente. Mi hermana podría utilizar un aparato (un espectrómetro) para obtener sus propios valores, pero como siempre preferimos transformar desde los míos.

A estos efectos, mi hermana debe proceder de nuevo a medir mi perspectiva desde la suya. Esto se traduce, como en el caso anterior, en que mide mis unidades (mis instantes), proyectándolas sobre las suyas (las frecuencias).

¿Cómo se come esto? Mutatis mutandis. Como ahora lo que medimos no es una distancia, sino una oscilación, no se mide con palos, sino -lógicamente- con osciladores. Concretamente, con un disco que rota, cuya representación es esta:

(Abajo en Anexo recuerdo por qué el número e, con este exponente, es un disco que rota)

Así pues mi hermana, si antes se situaba en su eje X y observaba la sombra que sobre él proyectaban mis metros X e Y, ahora lo que hace es ponerse en la rueda que gira a la frecuencia F y observar la sombra que sobre ella proyecta cada momento temporal T, esto es, anotar el lugar que ocupa el disco (lo que se llama la “fase”) en ese instante.

Acto seguido debe aplicar esta diferencia de perspectiva a mi medición de la señal f(x). Esto se traduce también en un producto de cada oveja con su pareja y suma de los resultados. Lo peculiar es que ahora los elementos son infinitos y continuos y por eso la suma de los productos es una integral. Para calcularla hay que evaluarla y esto requiere aplicar las técnicas del cálculo diferencial, pero tampoco hay que dejarse impresionar por estos términos, pues este cálculo es lo mismo que: en la versión más simple, coger el +10 y aplicarle un +d o un *r; en la multidimensional, coger cada uno de mis valores y multiplicarlos por un factor seno o coseno, a veces positivo y otras negativo, sacando al final el neto; de hecho ahora hacemos también esto mismo, con el matiz de que los resultados no miran simplemente a la derecha y a la izquierda, sino que apuntan en cualquier dirección y el neto lo sacaríamos (si es que pudiéramos hacerlo con infinitos elementos) mediante una suma vectorial, esto es, ligando todas las flechas (al extremo de una se junta la cola de otra) y trazando la raya que las une. El resultado será un número complejo que nos da la magnitud de la frecuencia y la dirección en la que apunta, su fase; con otras palabras, nos dice cuándo tiene que entrar cada frecuencia (cada nota) para acomodarse a la señal y en qué medida se acomoda.

Por fin, verán también un signo negativo en la fórmula, en el exponente. Para entender por qué conviene volver al ejemplo primero, el de la traslación. Allí todo se hacía sumando (es como se mide un objeto, cómo se mide la diferencia de perspectiva, cómo se aplica ésta…) y, por eso, para invertir la regla de conversión, para deshacer la suma, se restaba. Ahora lo que sucede en el exponente, la aplicación de las fases, también se traduce en una resta. Invertir es de nuevo cambiar el signo. Ahora bien, en qué transformación se pone el signo, en la de ida o la de vuelta, es una cuestión convencional y lo habitual es ponerla a la ida, como se refleja en nuestra fórmula.

Conclusión: he fracasado, quería explicar esto para niños y ni yo mismo lo entiendo, cuando lo intento leer al cabo de unos días, pero ¡que venga otro y lo perfeccione!

¿Y la conexión de esto con la muerte? Paciencia, ahora estoy muerto: ¡la próxima semana hablaremos de ello!

 Anexo: Por qué el nº e elevado a la i es un disco que rota

Como explicaba en otros posts, los números son adjetivos: cuentan una cualidad de las cosas, que es de cuántas unidades se componen. Pero son también adverbios, que nos dicen cómo hacer las operaciones con los números. Por ejemplo, yo puedo sumar 1 K, o sumarlo 2 veces (2K) o medio-sumarlo (1/2 K) o anti-sumarlo (-K). A esto, sumar conforme indica un coeficiente, lo llamamos multiplicar. Pero entonces la propia operación de multiplicar se puede efectuar de determinada manera, conforme indica un exponente. Por ejemplo, yo puedo multiplicar K por 2, o hacerlo 2 veces (K*2^2) o medio multiplicar por 2 (K*2^1/2 , que es raíz de 2)... Si multiplico el K por -1, tendré -K, es decir, habré girado mi K 180 grados; pero si lo medio-multiplico por -1, o sea, lo multiplico por raíz de -1... pues lo habré girado 1/4 de vuelta, 90 grados, lógicamente. De esta manera, lo que he hecho es mantener la magnitud del nº, pero darle una dirección totalmente independiente de la que tiene, una perpendicular a la original. A ese número que produce este efecto, raíz de -1, se le llama "i", la unidad "imaginaria", aunque se le podría haber denominado mejor la unidad perpendicular. 

Y ahora viene la gracia: ¿qué pasa si ahora este número i lo utilizo como adverbio? Por ejemplo, se lo pongo como exponente a un 2, como aquí 2^i, y entonces multiplico mi K "a la i", esto es, "a la perpendicular". Ojo: no lo estoy multiplicando por i, lo que tendría el efecto de girarlo un cuarto, sino por 2, pero "a la i". ¿Qué demonios es eso? Cuando multiplico una cosa por 2, la escalo dándole a cada una de esas unidades esa cualidad, pero en la misma dirección que ya tenía. Si ahora la multiplico por 2 "a la i", también la escalo, pero ya no para que crezca en su dirección originaria, sino para dotarle, también a cada una de sus unidades, de la dirección que en absoluto tiene, que es lo que significa perpendicular. Y darle a algo siempre dirección nueva es rotarlo, hacerle describir un círculo, que es lo que uno hace cuando está siempre cambiando de dirección.

El problema es cuánto arco se recorre. Para eso, hay que "normalizar", encontrar una unidad de escalado mediante rotación. La unidad de multiplicación longitudinal (de escalado en la misma dirección) es 2. La unidad de escalado mediante rotación es algo más, el nº e, que es  2,718 e infinitos decimales. De este modo, cuando se multiplica por e elevado a la i, resulta que se rota en arcos iguales al radio. O sea, si yo tengo un palo que mide K, pues al multiplicarlo por e^i lo roto en un arco igual a K, que es el radio de la circunferencia que K describe. Y como los ángulos de una circunferencia se pueden medir en arcos iguales a su radio o "radianes" (de los cuales la circunferencia tiene 2pi), habré rotado el K en un radian.

¿Por qué funciona así el número e? Se suele ejemplificar esto con el interés compuesto y continuo. Con un interés simple a tasa de 100% (esto es una velocidad de 1 K / año), lo doblamos, pero el nuevo capital lo dejamos aparte para sumarlo al final. Con un interés compuesto, seguimos doblando cada año, pero el nuevo capital no se aparta, sino que se acumula al antiguo, de forma que la 2º vez doblo 2, la 3ª 4 y así sucesivamente. Con un interés compuesto y continuo,  no esperamos al final de año para sumar el interés al capital, sino que se devenga y acumula en cada instante (ideal) del ejercicio (lógicamente por la parte proporcional), lo cual significa, a final de año, no doblar sino multiplicar por ese 2,718... (Para llegar a esta cifra se utilizan técnicas del cálculo diferencial, que aquí obviamos.)

Podemos decir así que la unidad de crecimiento de un interés simple es 1; la de un interés compuesto es 2 y la de un interés compuesto-continuo es 2,718... 

Si ahora cogemos esa unidad de interés compuesto continuo y le ponemos el exponente i, lo que sucede es curioso: el K rota, como manda el exponente i, y lo hace describiendo un arco a un tipo de interés del 100%, esto es, en una magnitud igual a su longitud, como si lo hubiéramos multiplicado por 2; ahora bien, ese efecto a lo largo del arco no se acumula y aumenta de forma compuesta y continua, sino que sigue la regla del interés simple, de forma que la próxima vez que multipliquemos por e^i lo que se volverá a doblar es el K inicial; ¿pero qué ha sido entonces de e y su efecto compuesto y continuo?; sucede que lo que actúa de forma compuesta (cada cambio de dirección opera sobre el acumulado anterior) y continua (en cada punto ideal) es solo el cambio de dirección. En suma, el ritmo de avance a lo largo del arco será siempre el K inicial multiplicado por el número que está en el exponente junto a i, es decir un cierto número de radianes; el resto del "efecto e" se consume en hacer que cambie la dirección de forma continua y compuesta. 

Joseph Fourier y la muerte (I)

 

Este verano he tenido dos ocupaciones intelectuales: las transformaciones de Fourier y la muerte. Y es curioso que al final se me ha mezclado la una con la otra.

Lo de Fourier se reduce a explicar que esta fórmula, que parece apabullante…

va simplemente de ver un problema desde dos perspectivas alternativas, el tiempo o la frecuencia, buscando la que mejor solución ofrece para cada tipo de problema.

Y he dado en pensar que la vida y la muerte son también eso mismo, las dos caras de una misma moneda, dos puntos de vista sobre el mismo problema.

Que haya tenido presente la muerte no es raro. La Parca nos ha visitado con insistencia, a causa del coronavirus, aunque (en punto a los detalles) hayamos mirado para otro lado. Al parecer, nuestros medios de comunicación acordaron no lanzarse a por imágenes de enfermos desasistidos o féretros amontonados. También nuestros gobernantes se abstuvieron de realizar campañas institucionales amedrentadoras, donde se nos instara a ser prudentes con imágenes truculentas. Supuestamente ambos actuaban por delicadeza y para aupar nuestra moral, aunque dado el historial de unos y otros, esto es difícil de creer. En el mundo moderno, priman las consideraciones comerciales y las electorales, así que probablemente se estimó que ser descarnado no era fuente de réditos, ni económicos ni electorales. No es extraño, porque nuestra cultura vive de espaldas a la muerte: nunca se habla de ella y cuando se planta ante nuestros ojos, enseguida la negamos, asegurando a los niños y a nosotros mismos que el muerto no ha muerto, porque sigue vivo en el cielo.

Parecerá chocante, porque últimamente venía hablando mucho de Dios, en el sentido laxo en el que yo manejo la palabra, pero hoy he tenido la revelación de que, sin lugar a dudas, no hay tu tía: cuando yo muera, desapareceré. Cualquiera, por religioso que sea, puede comprenderlo y admitirlo, si es honesto respecto del concepto de yo. “Yo” soy algo que es fruto de mis genes y mi educación y las vicisitudes de mi vida. Evidentemente, si mis células se consumieran en el fuego, pero siguieran dando guerra en el más allá, eso no solo sería inverosímil, sino desalentador: ¡pero, hombre, es que ni en el propio infierno me libraría de mis manías y mis miedos! Ya durante la vida, dejamos atrás muchos “yos”. Como decía Unamuno, somos un “cementerio de almas”, de las que nos hemos ido desvistiendo, queriendo o sin querer. Cuánto más, es lógico -y hasta deseable- que al morir las perdamos de vista, de una vez por todas. Se me dirá: “pero queda lo más esencial, el alma de las almas, el espíritu que de verdad somos y se levanta en el aire, fruto de una destilación que le despoja de todo lo material y grosero…” Sea así, si se quiere, pero esa cosa tan etérea, esos licores celestiales, no somos “nosotros”. Esos fantasmas, de tan esbeltos, no se diferencian apenas los unos de los otros y se confunden entre sí, como pedazos, si acaso, de un espíritu universal. Pero a mí lo que me rompe el corazón no es que se marche una esencia. A mí lo que me abruma es la pérdida de lo material y lo concreto: que un muñeco de carne y hueso, al que aprecio, se desvanezca y me deje sin su compañía. Lo que me acongoja ahora, en mi madurez, es pensar que el tiempo de mi propio muñeco se puede acabar y el final me pille sin haber hecho mis deberes, las cosas que quería construir en la vida…

La muerte, pues, no deja de ser una verdad, una dolorosa verdad. Parece lógico por tanto mirarle a la cara, pues aceptar lo que es (en el sentido de “verlo”, sin negar su existencia) siempre ayuda a sobrellevarlo. Recientemente oía a la humorista y presentadora Paz Padilla hablar de la muerte de su marido, por efecto de un cáncer. Ella le ayudó a morir. Tuvo la clarividencia para comprender que también para eso hay una técnica. Y sacó de su interior la presencia de ánimo requerida para estudiarla y aplicarla, proporcionando a su pareja el ambiente (tranquilidad, luces, música…) y el cariño que ayudan a marcharse en paz. Yo lamento mucho no haber sabido eso y no haberlo hecho cuando puede hacerlo. Mi madre murió de otro cáncer ya en sus ochenta, aunque ella estaba por lo demás muy bien conservada y con ganas enormes de vivir. Cuando ya fue irremediable, prefirió y preferimos que pasara en casa esa fase terminal. Mi hermana y yo la atendimos mucho. Sin embargo, hubo un día postrero en el que estaba ya muy fatigado y me fui a dormir a mi casa. De alguna manera, sabía que era el último, pero me sentí justificado para descansar. A la mañana siguiente, la señora que la cuidaba nos dijo que, en efecto, mi madre había muerto de madrugada.  Me quedé con la pena de no haberla acompañado en esos instantes. También de alguna manera fallé con mi cuñado. Le pasó otro tanto de lo mismo: después de idas y venidas de otro cáncer, un día tuvo  un shock y a partir de ahí lo atendieron en casa, hasta el final. Uno de los últimos días fuimos a verle. Sí lo saludé al principio. Estaba como ya muy débil y ausente, pero consciente. Mas, después de comer, mi mujer y mis hijas le volvieron a ver y hasta le hicieron reír. Y a mí, todavía no sé por qué, me dio por decir: “no, prefiero no verle otra vez, me da mucha pena recordarlo así, prefiero preservar la imagen de cuando estaba bien…” Qué estupidez, qué egoísta fue eso: el tema no eres tú, ni la tontería de conservar una imagen u otra; el tema es que alguien se muere, se descabala su muñeco, y hay que confortarlo…

En fin, qué se le va a hacer, procuraremos hacerlo mejor en adelante, con los otros si fuera el caso (Dios no lo quiera…) y con uno mismo, pues como es sabido todos los días vivimos y morimos un poco. Aquí es donde el otro asunto, el del tiempo y la frecuencia, reaparece y resulta iluminador. Pero eso lo dejo para otro post, pues me he convencido de que es buena práctica hacerlos más cortos y digeribles.

Sabias mentiras

En estos tiempos de Coronavirus, que invitan a la lectura (con permiso del teletrabajo) he seguido la recomendación de mi hija sobre un libro que es del estilo de los que yo le recomendaría a ella: Homo Sapiens.

Veo ahí reflejada esa teoría de la que tantos se han hecho eco y que mismamente mencionaba en mi último post: la idea de que las invenciones o ficciones pueden ser muy loables, por falsas que sean, si animan a la acción, a una acción positiva. Pero lo que el libro tiene de llamativo es que enlaza lo anterior con la evolución. El autor sostiene que nuestra especie, el Homo sapiens, pega el salto evolutivo que la aúpa al dominio de la tierra, cuando desarrolla la capacidad no sólo de comunicarse, mediante el lenguaje, sino de mentir con el mismo. Prosperamos, no porque podamos advertir al vecino de que viene un león, o mencionar cualquier otra cosa tangible, sino cuando parimos ideas abstractas, que no se refieren a nada que exista: cuando creamos un ídolo como el de la escultura de la imagen, dioses y demonios, infiernos y paraísos, instituciones, naciones o ideales como la  fraternidad, los derechos humanos o la democracia... Y ello porque esas quimeras tienen la virtud de impulsarnos a actuar y sobre todo de hacerlo cooperativamente, aunando a decenas o cientos o miles y miles de personas en torno a un fin común. Son mentiras, pues, pero mentiras prácticas. Lo que hay que ver, sin embargo, como decía antes, es si esa acción concertada es positiva o negativa, si trae un mundo mejor o lo empeora.

Es curioso que esta tesis tiene buena prensa cuando se trata de atacar: cuando se aplica para desmontar mentiras dañinas. Leía antes de este libro el de Vargas Llosa, Tiempos recios. Denuncia
este volumen cómo un acto de propaganda, orquestado por la multinacional United Fruit, consiguió en los años 50 convencer a EEUU y al mundo entero de que el gobernante de Guatemala era un peligroso comunista, cuando al parecer el pobre hombre (que al final fue derrocado y tuvo un triste final) era solo un reformista bien sensato, que buscaba instaurar en su país una democracia "a la americana".

Está bien esa denuncia y máxime si viene de la linda mente y con el lindo envoltorio de palabras de un pensador tan agudo, por cierto injustamente denostado (otra fea mentira) por quienes le acusan de haberse tornado conservador, cuando lo que es, simplemente, es una persona con sentido común... Mas no nos desviemos del tema. Decía que no lo niego: hay que airear las mentiras que nos llevan al error, que hacen peor el mundo. Pero lo que no tiene tan buen cartel es ensalzar una idea benigna, una que sirve para redimirnos y, pese a todo, reconocer que es una pura invención.

Con esta ceguera me he enfrentado esta semana, en mi profesión jurídica. Para salir de un atolladero legal, he propuesto un cuento, una comedia, una narración. Se trata de acordar con la contraparte que vamos a acabar allí, pero para eso yo le pido que tal y él me contesta que cual y al final nos arreglamos con una solución transaccional, lo cual las autoridades verían como muy razonable y no nos buscarían unas cosquillas que, de otra manera, en ausencia de esta representación, nos encontrarían. "¿Es esto un fraude de ley?", les dije yo mismo. "No", les contesté, antes de que mis interlocutores pudieran salir de su estupefacción, "porque es una representación que refleja el patrón de conducta correcto, el modo en que deberíamos habernos comportado, a la vista de las circunstancias excepcionales que nos rodean (precisamente, las del virus). Si por pereza mental, por inercia, actuáramos como lo haríamos en circunstancias normales, estaríamos construyendo otra patraña también, pero una perjudicial a nuestros intereses". ¿Qué cosa más razonable, verdad? Pues no hay quien lo entienda en mi entorno. Unos por ser "personas ingenieras" y otros por ser "personas europeas del norte" (y por ende, me temo, algo "personas calvinistas")... el caso es que a todos se les escapa el razonamiento.

Y es que, en efecto, lo bueno, en la mentalidad oficial y bienpensante, tiene que ir unido a una protesta de verdad. Tiene que ser un descubrimiento de una especie de matemática oculta entre los átomos, que no admite réplica. No puede ser una creación, un acto de voluntad y, sobre todo, pragmático, con el que se trata de realizar un objetivo, por vericuetos más o menos debatibles. Ah, pero ahí interviene la propia Ciencia, representada por la biología evolutiva, para darle en las narices a los ortodoxos: la verdad científica es que, en nuestra propia naturaleza como Homo Sapiens, grabado a fuego en nuestros genes, ¡está que hemos de fabular siempre, para bien o para mal!

Homo conceptualis, precisamente, es una expresión que se me ocurrió hace tiempo, para poner de manifiesto que los humanos vemos la realidad a través del cristal ahumado de conceptos, lo cual es malo, porque distorsiona esa realidad y conduce al absurdo de matar o morir (o dejar de vivir...), por mor de defender castillos en el aire. Por eso sugería que sapiens era un título prematuro, que aún no merecemos y que habría que reservar  para una especie futura, aún embrionaria (véase aquí). Pero ahora este libro me recuerda que la sabiduría también va unida al concepto, que todo lleva aroma de mentira, lo bueno y lo malo... Así sea, pues. Amen.

Nos conduce esto a otro de mis temas queridos, el de Dios. Hoy he tenido, al hilo de estas reflexiones, una epifanía: el famoso problema de "creer que Dios existe o no existe" es, como tantos otros, un falso dilema. La razón es obvia: hay que creer en Dios ¡precisamente porque no existe!

Y me explicaré muy bien, sin esperanza de convencer sobre la bondad de la idea ni a los ateos (que estarán de acuerdo en la inexistencia del sujeto, mas no en la extrema utilidad del concepto) ni a los creyentes (que alabarán el concepto, pero se escandalizarán ante el componente que de mentira tiene).

Me inspiro en el concepto de Dios de Joel Osteen, un predicador americano, que oficia en lo que fue el viejo estadio de los Houston Rockets y concita una enorme audiencia televisiva. Esta descripción del sujeto espantará a muchos, pero puedo asegurar que es un chico excelente. A mí, por lo menos, me encanta oírle y verle en YouTube.

Joel se apoya en pasajes bíblicos del Viejo o Nuevo Testamento como lo que son, metáforas que comunican un mensaje, mas lo hace siempre con un objetivo práctico, nada fanático: no condena conductas sexuales, ni busca adhesión a dogmas incomprensibles, ni tampoco la confrontación política; sólo quiere que la gente tenga fe en sí misma, confianza ante las adversidades, disfrute de la vida y sea compasiva. Podría pasar pasar por un simple psicólogo, otro gurú de la auto-ayuda, si no fuera porque la clave de su receta es creer en Alguien, un Dios que es... Bueno, no pretendo en este post reproducir la "teología" de Joel. Queda para otras ocasión, quizá. Solo resaltaré lo que aquí interesa: que ese Alguien no existe.

En efecto, es un Padre que confía a ciegas en nosotros; nos manda adversidades, es verdad, pero al objeto de enseñarnos a ser fuertes y humildes y compasivos; nos obliga a desarrollar "músculo espiritual", porque tiene grandes planes para nosotros, en los que seremos líderes, mas líderes en servicio; y quizá seamos ricos, mas no en bienes de este mundo (si bien tampoco nos los quitará,  si son instrumentales), sino en fortaleza y paz interior; en este camino, podemos cometer los peores errores; de paso a la integridad, quizá seamos ladrones; antes de sencillos, soberbios; antes de puros, lascivos; nada importan los rodeos, el Padre los perdona, porque sabe que nos hallamos under construction; y lo mismo que Él es indulgente, otros nos juzgarán y reprobarán, pero no ha de importunarnos esto, porque solo a Él (es decir, a su plan para nosotros) debemos complacer.

Pues bien, mire Usted a su alrededor. ¿Existe Alguien así, que le tenga en tan alta estima, que a tan alto quiera encumbrarle, a quien no le importe de tan bajo sacarle y a quien pueda mirar siempre, con la certeza de recibir su apoyo y su guía? Evidentemente, no. Ah, yo pienso mucho últimamente en mis padres. Fueron buenos y fueron gente especial. Tengo muchas ganas de escribir algo sobre ellos... Pero eran humanos y, como todos nosotros, fallaban y un día faltaron. El Padre no tiene estos hándicaps: es inmortal, todopoderoso e infalible y nunca deja de trabajar a nuestro favor, con el máximo tino. Así las cosas, no hay espacio para la duda. La empresa de la vida, de una vida plena, es demasiado importante como para dejarla al albur: si existe un recurso que garantiza el éxito del viaje, hay que pertrecharse con él... No seamos puntillosos, porque nos jugamos demasiado. Cosas que son de tan ventajosas, casi imprescindibles, no las podemos poner en riesgo por un quítame allá esas pajas, por la tontería de si "existen o no existen".

Ahora bien, naturalmente, al que no le guste este concepto de Dios, que lo diga y -parafraseando a Groucho Marx- miramos a ver si se podemos inventar otro mejor, pues si así fuera, sería divino... Y quien, pese a todo, no esté conforme con este proceder, podrá irse ufano, mirándonos condescendiente, porque necesitamos agarrarnos a una ficción para sobrevivir. Y se irá tranquilo, acariciando con todo derecho -como buen Homo sapiens- su propia mentira, la de su preferencia...

Nuevos Blogs

He decidido pasar los comentarios más técnicos a otros Blogs especializados:

- Los de temas de Física y Matemáticas, al que ya tenía en inglés, el cual después de unos cuanto años he reanudado, con una entrada sobre las derivadas: https://fairyconcepts.blogspot.com/2019/12/derivative-as-rail-for-growth.html

- Los de Derecho a uno nuevo, que llamo "Dolo bueno" y en el que he empezado escribiendo un post sobre la situación de prisión del Sr. Junqueras, tras la sentencia del Tribunal de Justicia de la Unión Europea: https://dolobueno.blogspot.com/2019/12/junqueras-no-es-el-agente-007-ni-es.html

Lo que digo sobre Derecho es bastante fiable, ya que esa es la especialidad que siento que domino. El título que he elegido para el Blog, "Dolo bueno" (la expresión se suele emplear en latín, dolus bonus, pero estaba ya en uso para blogspot), alude a la lícita exageración de las bondades de su mercancía que puede hacer un comerciante, sin que ello supongo engaño. También al hacer ciencia jurídica, uno puede barrer algo para casa, hacia las soluciones que prefiere. Pero lo que es feo es manipular los conceptos, aprovechar sus oscuridades para crear confusión, utilizarlos de forma demagógica, etc. Por lo menos garantizo que en ese Blog yo no incurriré en el dolo malo del conocimiento, si acaso en el bueno.

En cambio, lo que digo sobre Ciencia hay que tomárselo con prevención (with a grain of salt, como dicen los ingleses), porque ahí soy amateur.

De este modo, reservo para este Blog la parte más creativa, que es la de sacar de su lugar los conceptos y utilizarlos en otras áreas, pero sin necesidad de entrar en detalle sobre los aspectos técnicos, para los que puedo remitir a los otros cuadernos.

Paz más territorios

Antes de seguir con lo de las transformaciones matemáticas, he decidido dejarlas tranquilas un rato, para hacer un inciso: un paréntesis precisamente sobre la paz. En estos tiempos convulsos, el filósofo debe decirse: “bien, hay problemas, reivindicaciones, discrepancias, afrontémoslos si desean ustedes, pero no conseguirán turbar mi paz”. Y lo que es más importante: esto no hay que objetárselo tanto a los demás, a los que gritan en la calle, como a uno mismo, a ese piquete de personajes que suelen vociferar en el interior de la cabeza. Unas voces advierten sobre peligros, para que nos preocupemos; otras nos piden satisfacer deseos, como si nos fuera la vida en ello. A todas se las oye (esto es inevitable: simplemente sucede), pero no necesariamente hay que pararse a escucharlas y desde luego no hemos de permitir que nos alteren.  Pues al fin y al cabo, es mucho más lo que perdemos si les entregamos nuestra paz de espíritu. Eso sería como si uno saliera a la calle con un gran tesoro en la mano y lo tirara a la alcantarilla al menor contratiempo.

Lo paradójico es que, según dicen los expertos, merced a esta receta, las cosas de la vida también evolucionan mejor: al final llegan menos males y más bienes, como por arte de magia; la paz, trae debajo del brazo, nuevos territorios.

Mi muy querido cuento de Cenicienta lo ilustraba muy bien. Cuando la muchacha se entera de que sus hermanastras se acicalan para acudir al baile organizado por el Príncipe, donde elegirá esposa, la madrastra le hace una jugada perversa: vendrás con nosotras, le espeta, solo después de recoger los miles de lentejas que la muy capulla desparrama por el hogar. En este trance, sin embargo, aunque Cenicienta llora como primera reacción, no desespera y se aplica a trabajar. Mientras lo hace, sin darse cuenta, advierte que miríadas de pajarillos acuden en su ayuda y completan por ella la ingrata tarea. Entonces es cuando se presenta el hada madrina, que le da vestidos y carrozas y a partir de ahí ocurre cuanto es sabido.

Desde una perspectiva religiosa, se afirma algo semejante. Se predica: dale tus problemas a Dios y quédate en paz; trabaja (¡sigue con el mazo dando, aunque estés rogando!), pero hazlo con alegría, porque, si te conmueves y arrebatas (si, como se dice hoy, te estresas), Dios se sale del juego: es como si las olas que generas con tu desasosiego crearan una pantalla en la que rebota; pero si confías en Él, en el plan que tiene pergeñado para tu vida, Él y sus ángeles (trasunto, obsérvese, de los pajarillos) moverán los hilos con pericia, os guiarán a ti y a tu entorno para que las cosas casen. Y si las cosas no casan o tardan mucho en casar, pues será que “no está de Dios” que así sea, de forma que no hay razón para alterarse ante lo inexorable, no hay motivo para dejar de disfrutar con alegría de la existencia, mientras dure.

Un ateo, sin embargo, advertirá:  ¿para qué inventar hadas del bosque en el fondo del jardín? No es preciso imaginar fuerzas sobrenaturales para explicar lo que tiene una lectura racional. Se trata simplemente de que el subconsciente contiene un arsenal de recursos con los que puede ayudarnos y hay que dejarle trabajar. El estado de relajación es campo propicio para que funcione, mientras que la turbación lo bloquea. Los pajarillos y los ángeles valen como metáfora, pero son en realidad agentes materiales.

A mí la verdad me vale tanto lo uno como lo otro, si funciona igual, a efectos prácticos. Como dice el título de la peli del ahora denostado, pero aún tan querido Woody Allen: Whatever works. La cuestión es, no obstante, si funciona igual lo uno que lo otro. ¿Nos da tanta paz creer que tenemos a nuestro servicio a fuerzas mágicas, o a un Dios todopoderoso, como leer Scientific American Mind, por mencionar una publicación que habla de estas cosas? ¿Sin la fe en lo sobrenatural, no se pierden la ilusión, la expectación, las mariposas en el estómago que mueven montañas? 

Si escuchamos por ejemplo al biólogo inglés Richard Dawkins, la respuesta es clara: en absoluto. Según él, para sentir tranquilidad de espíritu y hasta un punto de arrebato místico, basta contemplar la belleza del universo y lo pasmoso de la vida y cultivar las emociones que ello genera. Hay una espiritualidad atea, que puede llenarnos de gozo y de consuelo. Para ilustrarlo, en su libro El espejismo de Dios, pone como ejemplo cómo él y sus amigos despidieron a un colega al que venció la enfermedad. Se reunieron en una especie de servicio laico: pronunciaron discursos y se emocionaron cuando uno de ellos tocó la gaita. Podemos imaginar al gaitero tañendo su instrumento entre brumas y tocado él mismo con uno de esos “morriones”, esos gorros altos de piel de oso que llevaban los granaderos y que tanto gustan a los anglosajones...

Naturalmente, estoy de acuerdo con Dawkins. No estarlo es de hecho una actividad de riesgo, porque el tipo tiene una lógica demoledora y un verbo afilado. Pese a todo, añadiría dos cosas que no contradicen lo anterior, una formal y otra de fondo.

En punto a formas, la elección de la ceremonia que nos enganche es cuestión de gustos y por ende subjetiva: no hay nada escrito. Yo respeto lo del gaitero, pero tampoco es un canon obligatorio, obviamente. Si en cualquier religión encontramos imágenes o ceremonias que nos aportan paz, bienvenidas sean.

La observación de fondo es que, por supuesto, cualquier modelo debe pasar el filtro de la razón, no hay revelación que nos deba inducir a hacer cosas que a nuestra razón repugnan, pero -sentado lo anterior- tampoco es exacto decir que las hadas o los ángeles son un modelo de interpretación del mundo “irracional”. La Ciencia no consiste más que en eso, en parir modelos que no explican todo y ni siquiera pretenden explicarlo, aunque hoy por hoy funcionan en la práctica. Esto lo argumentaba muy bien un tal Epstein en un libro sobre relatividad (Relativity visualized): en la antigüedad hubo uno que dijo que la Tierra se mantenía en el espacio porque la sostenía un gigante y, bueno, lo cierto es que a partir de ahí vivíamos tranquilos; luego Newton parió la idea de la gravedad como un efecto que causa la masa y determina la posición de los astros; ahora -afinando- se dice, con Einstein, que la gravedad la causa la curvatura del espacio-tiempo y con eso se hacen cálculos cosmológicos muy exactos; pero falta aunar la relatividad general con la cuántica y vaya usted a saber qué modelo nos depara el futuro. El mensaje a retener es que los modelos de cada momento nunca dicen cómo es todo, sino que ofrecen una metáfora y nos piden que funcionemos como si las cosas fueran así (el famoso as if…). El único requisito para validar un modelo como científico es que no haya otro que, en la práctica, funcione mejor: otro que resuelva más problemas de la vida real.

Sobre esta base, volviendo al tema concreto que nos ocupa, el de la paz, yo lo que pediría es que el modelo tenga un componente afectivo y uno de dirección, por la sencilla razón de que eso funciona mejor.

Reconozco que hay un mérito enorme en el filósofo estoico que predica un desnudo amor al destino (el  llamado amor fati), sin necesidad de adornarlo con nada más. Pero a mí, con eso, me falta un empujoncillo.

Para ilustrar esta carencia, acabo de hacer una búsqueda en internet sobre aquella expresión y aterrizo en este sitio que a su vez contiene dos citas:

Mi fórmula para expresar la grandeza en el ser humano es el amor fati [amor del destino]: no querer que nada sea distinto ni en el pasado ni en el futuro ni por toda la eternidad. No sólo soportar lo necesario, y menos aún disimularlo...sino amarlo.

(Friedrich Nietzsche)

[Es imprescindible] no querer nada más que lo que es. [...]Oh mi Dios, todo lo que proviene de tus diseños me conviene. Nada es demasiado pronto ni demasiado tarde para mí, si está en tu tiempo.

(Marco Aurelio)

En cuanto a la diferencia entre ambos textos, no le daría demasiada importancia al hecho de que Marco Aurelio hable de un diseño y sugiera la existencia de un diseñador. Lo que me importa es que habla con alguien, al que se dirige con emoción. Quién sea y cómo sea ese alguien, me da más igual. Puede ser simplemente el resto de la gente o el resto del universo, pero en todo caso es algo con lo que se mantiene un diálogo cálido, a veces con los sentidos y quizá también de forma inconsciente (conectando con el inconsciente colectivo, por canales que hoy por no conocemos bien, pero podrían existir).  Y luego está la fe en que lo que trae el destino nos conviene, ha de ser a la postre un bien. Todo ello está implícito en la idea del amor al destino, pues ésta sin querer denota un cuerpo al que abrazar y que nos devuelve amor, pero no está de más explicitarlo en el modelo: deberíamos amar nuestra suerte como si fuera alguien y como si fuera alguien que nos corresponde con su amor. Así visto, da más paz.

Y, si no tenemos prejuicios antirreligiosos, podemos adornar la idea con citas de maestros, en el bien entendido (ocioso es decirlo) que esto no comporta que condenemos el matrimonio homosexual ni la despenalización del aborto… Jesús habló de no tener ansiedad por el mañana, de vivir al modo de los lirios o los pájaros del campo. A Pablo, cuando visitó Filipos, le dieron una buena paliza y lo encerraron en una mazmorra, pero pasó la noche bien, cantando alabanzas a su suerte y al Señor, hasta que a la mañana siguiente un terremoto abrió las puertas de la prisión. Y definió su sensación nocturna, que tan bien le funcionó, como una “paz que supera…” Lo que supera, en el original griego, se llama noûs y admite dos interpretaciones. La que ha prevalecido es la superlativa: a quien rebasa esta paz es a nuestro entendimiento; esto es, estamos ante una paz tremebunda, que nos deja pasmados. La otra lectura es que la paz vence a su oponente, que son los pensamientos. La verdad es que, si investiga uno sobre el significado del término en la filosofía griega, parece que la primera interpretación sea más plausible, porque con noûs se alude a las facultades superiores del intelecto, cercanas al alma. Sin embargo, me gusta la segunda lectura, porque -aunque sea de chiripa- apunta a lo que probablemente mata la paz. Resulta que, al parecer, nuestro cerebro funciona por defecto (es el llamado default mode) tocando las narices, para cabrearte contra el destino. La meditación, que proporciona el antídoto, consistiría en hacer uno acto de presencia para pillar in fraganti a ese default mode y simplemente observar: “ah, es él otra vez…”

Puedo afirmar que algo, algo, esto me está funcionando, mas se requiere esfuerzo y disciplina para consolidar el hábito. ¡Sigamos trabajando!

Transformaciones entre hermanos (I)

Voy a empezar a compartir lo que he venido pensando últimamente sobre las transformaciones entre sistemas de coordenadas. Lo haré de una manera “literaria”, que debería espantar más a los científicos, aunque estoy convencido de que será al revés: a lo mejor aquellos lo tragan, pero raro será el que, siendo de letras, se pare en esto. ¿Por qué la gente de Ciencias es más multidisciplinar y puede gustar de y hasta escribir una buena novela o un poema, mientras que a los literatos les ahuyenta una ecuación? No lo sé, pero vayamos al grano. 

Mi propósito es demostrar que un razonamiento muy simple que hacemos todos los días contiene todas las claves para entender, vía analogía y esa recurrida técnica que es el mutatis mutandi, ecuaciones aparentemente complejas.

El razonamiento de todos los días es: para T la casa familiar se encuentra a 10 m; su hermano Ω se coloca 3 m a la derecha; luego respecto de este último la casa está a 7 m.

Las ecuaciones más complejas son:

El método analógico, que sirve para llegar desde lo uno a lo otro, es el que definía en posts anteriores y desarrollo aquí:

• Uno se fija en la situación de partida, vuelve la mirada a la nueva y concluye a primera vista: se parecen como un huevo a una castaña.
• Sin embargo, nos empeñamos en hallar una similitud entre ambas cosas, que nos ayude a digerir la segunda. ¿Pero dónde hay que buscar el parecido? ¿En el color, en la forma? ¿Acaso en el olor? ¿Por ventura en el sexo? En Derecho lo tenemos claro: existe analogía si hay “identidad de razón”. Quiere esto decir que la similitud se localiza (o no) en la ratio legis o ratio decidendi o razón de ser o espíritu de la disposición... Lo cual suena pomposo, pero a la postre no es más que el objetivo práctico que se persigue al promulgar la norma. Y esto que se hace en Derecho, se debe hacer siempre, pues al fin y al cabo todo concepto es una forma de resolver un problema de la vida real. Así, por ejemplo, si el objetivo es comer, el huevo y la castaña son análogos y encajan en el concepto abstracto de alimentos; mientras que si el fin es alimentarse dentro de dos meses, ahí cesa la analogía, porque el huevo es más perecedero.
• Una vez identificado este objetivo y suponiendo que es común, hay que seguir trabajando a nivel de detalle. El huevo y la castaña son muy elementales, pero otras situaciones resultan complejas, esto es, se componen de múltiples elementos y en todos ellos hay que separar la paja (lo concreto) del trigo (lo abstracto). En efecto, cada componente admite dos formulaciones: una es la específica, ligada a su particular contexto (“cáscara de huevo”; "piel de naranja"), y otra es la abstracta o delgada, que abarca múltiples objetos (“protección del alimento”). Algo así como la diferencia aristotélica entre lo accesorio o accidental y lo sustancial o esencial. Pero ello, en el bien entendido, insisto, de que qué sea lo esencial y qué venga a ser accesorio no es ni mucho menos algo “consustancial”, que acompañe a las cosas por doquier, sino que depende del espíritu; esto es, de para qué rayos queremos esas cosas.
• Así pues, la labor de destilación se asemeja a una mirada de rayos X que traspasa lo concreto para ver en sus entrañas la esencia generalizable, en uno y otro lado. Ahora bien, no se trata solo de centrarse en lo abstracto y olvidar lo concreto, pues el mutatis mutandi también sirve para entender mejor cómo funciona lo particular. No basta decir, “bueno, esto es como lo otro y ya está”. También hay que intentar captar lo que podríamos llamar la “diversidad de razón”, que hace que la regla general juegue de forma distinta, se module y se retuerza en cada lado. De la misma manera que los términos de la comparación tienen un espíritu común, también tienen otro discrepante. Y ver ese diablillo es importante, porque sirve para adivinar qué debe cambiar en el nuevo contexto y cómo debe cambiar: qué otros presupuestos son exigibles o qué nuevas consecuencias se aplican…
• Por fin, como también contaba en otro sitio, al realizar esta tarea, a veces se producen sorpresas. Sucede que, al abordar lo complejo, uno advierte que se había dejado en el tintero algunos elementos que definen lo sencillo, porque de tan evidentes los daba por hechos. Y así puede establecerse una comparación más exhaustiva, que ilumina ambos lados.

Dado que yo ya he hecho este viaje de ida y vuelta, paso directamente a definir la situación de partida sencilla, pero de modo completo:

•          T ha medido que la distancia a la que se encuentra la casa es [S]_T = 10 y queremos adivinar el valor [S]_Ω, esto es, qué mediría Ω. (Entre corchetes pongo el objeto que se mide. El subíndice representa desde qué perspectiva se mide el objeto.)

• Ruta A) o directa: El hermano nuevo Ω mide la posición del viejo T y advierte que está situado a distancia  [T]_Ω =  -3 m de su propia posición. Razona así: T piensa que es el centro del universo, pero en realidad el centro soy yo y él se encuentra, digamos, corrido a la izquierda. Por eso, todas sus mediciones están teñidas por tal defecto de visión (mide 3 m de más en todo lo que se encuentra a su derecha, 3 de menos en lo que se halla a su izquierda…). ¿Solución?  Corregir sus valores añadiendo ese mismo -3, con lo cual consigo que el resultado sea idéntico al que habría medido yo. La regla de transformación es, por consiguiente:

[S]_Ω = [S]_T + [T]_Ω = [S]_T +(-3) = 10 - 3 = 7

•         Ruta B) o indirecta: Es T quien mide la posición de Ω y advierte que está situado a distancia [Ω]_T =  +3 m de su propio lugar. Razona así: Ω mide desde +3 y por eso si yo quisiera transformar su medición sobre dónde está la casa tendría que añadirle ese +3, mediante la siguiente fórmula:  

[S]_T = [S]_Ω + [Ω]_T = 7 + 3 = 10

Pero yo no quiero eso, busco lo contrario: se trata de ser empático, ponerme en la piel de Ω para traducir mis propias mediciones a su perspectiva. Debo por tanto invertir la regla de transformación que acabo de identificar, para que le valga a mi hermano A este fin, advierto que Ω no va a discrepar sobre el valor absoluto de la distancia que nos separa, que es |3|, porque esto no se ve afectado por el punto de vista: el palo con el que medimos no se contrae ni se dilata por el hecho de blandirlo desde distinta posición... Ahora bien, lo que sí cambia es la orientación: yo veo a Ω a mi derecha, él me ve a su izquierda.   ¿Solución? Debo cambiar en la fórmula aquello que representa la orientación, esto es, el signo. Llego así a la misma solución que proporcionaba la Ruta A):

[S]_Ω = [S]_T +(-[Ω]_T) = 10 +[-(+ 3)] = 7

¿Cuál es aquí entonces el problema práctico que se plantea? Hombre, si decimos que el problema es cuánto tienen que andar el hermano T o Ω para llegar a su casa, entonces tenemos dos trabajos distintos, ya que (aunque ambos hermanos comparten la misma regla o cinta de medir) cada uno parte de un origen diverso. En cambio, en las situaciones que veremos más tarde, los hermanos están plantados en el mismo origen, aunque lo que altera su perspectiva es el hecho de que han de utilizar no uno, sino varios instrumentos de medición (cuyos valores anotan en ejes de coordenadas) y estos “sistemas de coordenadas” tienen diferentes orientaciones (no están desplazados o “trasladados” sino “rotados” entre sí). Su problema es, por tanto, el mismo. Pero lo que es común en todos los casos es el problema que podríamos llamar “lingüístico”: si alguien con sus instrumentos ha hecho unas mediciones y obtenido unos valores o coordenadas, ¿cómo se traduce esto al lenguaje de otro que tiene una perspectiva diferente?

Identificado así el desafío, como un “problema de traducción”, el ejemplo de la traslación es muy ilustrativo, porque ofrece una solución abstracta sencillísima:

•        Un hermano debe medir la perspectiva del otro, haciendo lo mismo que hace para medir el objeto analizado.
•           Esa medición de la perspectiva ajena sirve como regla de transformación para traducir también las coordenadas relativas al objeto analizado.
•         Ahora bien, si el que mide la perspectiva de su colega es Ω, el hermano de destino, su medición vale sin más como clave [ruta A) o directa]; en cambio, si es al revés, si mide T, el de origen, éste debe invertir la regla [ruta B) o indirecta].

A partir de aquí, esto es como lanzarse en un tobogán: basta aplicar esos sencillos trucos y se aterriza como quien no quiere la cosa en los brazos de Lorentz o Fourier, comprendiendo sus ecuaciones. Sin embargo, debo decepcionarles, porque me saldría un post enorme e infumable si lo explicara todo de corrido. Serán necesarias varias etapas, aunque comprendo su impaciencia y prometo volver pronto con nuevas entregas de esta historia, esta apasionante historia.