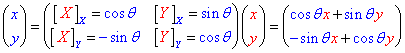Joseph Fourier y la muerte (II)

 

Retomando el tema que dejé apuntado en la entrega anterior, a continuación paso a explicar por qué están conectadas las transformaciones de Fourier con la muerte. Como siempre, intentaré ser ameno en la parte matemática y animo a digerirla, porque el final que reservo (la conexión entre los binomios vida-muerte y tiempo-frecuencia) es en verdad impactante.

Partimos de un problema práctico, como la distancia hasta un gato. Desde mi posición, mido que el gato está a x = 10 m. Mi hermana se halla en un punto intermedio. Ella podría hacer su propia medición, pero preferimos adivinarla por lógica, “transformando” el valor que yo he medido. En concreto, mi hermana razona así: Javier sitúa el origen de su cinta de medir (el punto 0) en su propia posición, pero yo lo coloco en la mía y para mí él se encuentra a una distancia d = -5 m; por tanto, debo añadir a sus valores lo que él, desde su posición, juzga no tener, pero desde la mía sí tiene. O sea, x = x + d = 10 + (-5) = 5 m. 

(Ya sé que a ustedes les resultaría más comprensible que mi dilecta hermana razonara así: Javier, que está más lejos, cuenta 5 m de más, que yo debo restar; y si fuera al revés, si yo estuviera entre mi hermana y el gato: Javier, que está más cerca, cuenta 5 m de menos, que yo debo añadir. Pero, señores y señores, hay que encontrar una expresión común a ambas hipótesis y esa es la que he propuesto: Javier, desde mi posición, tiene lo que sea -positivo o negativo-, pero no lo computa, pues él cree que no lo tiene; por eso, para traducir sus valores a mi posición, yo tengo que "añadir" a los suyos esa posición que a mi juicio les falta -lo cual se traducirá en suma o resta, respectivamente-.) 

Alternativamente, yo podía haber medido la posición de mi hermana (d = +5). ¡Pero cuidado! Esto me valdría para transformar sus valores a mi lenguaje. Pero, si lo que pretendo es “ponerme en su piel”, debo darle la vuelta a mi medición, cambiándole el signo, lo que nos lleva a la misma regla de transformación: - d = - (+5) = -5 = d. Por cierto, puedo comprobar que el cambio de signo funciona porque, si sumo las dos reglas, la de ida y la de venida, vuelvo al punto de partida: d + d = 0.

Para aplicar esta idea a otras situaciones, debemos generalizarla. En lugar de “posición”, hablemos de “perspectiva”. “Medir la posición del otro” será por tanto “medir dónde queda la la perspectiva del otro desde la mía”. A esto le llamo, abreviando, “medir el cambio de perspectiva”. Y en lugar de “añadir” ese cambio al valor ajeno, podemos hablar de “aplicarlo”, lo que se traducirá en la operación aritmética que corresponda. De igual modo, si soy yo el que mide la diferencia de perspectiva, ya no le “cambiaremos el signo” sino que la “invertiremos”, de la forma que proceda: haremos lo necesario para que, “aplicando” a una regla su inversa, el resultado sea siempre “no hacer nada, dejar las cosas como estaban”.

Podríamos directamente emplear esta formulación abstracta para entender la transformación de Fourier, pero quedará más claro si pasamos por otros dos ejemplos intermedios.

El primero es el que podríamos llamar multiplicativo, en vez de aditivo. Supongamos ahora que mi hermana y yo compartimos el mismo origen, pero medimos con distintas unidades. Las mías son de 1 m, mientras que las suyas miden el doble, 2m. Ahora pues la perspectiva es el tamaño de nuestras respectivas unidades. Por tanto, cuando mi hermana mide el cambio entre tales perspectivas, lo que hace es comprobar que las mías son la mitad de grandes que las suyas, esto es, que la ratio entre ellas es ½ (r = ½). Aplicar esta regla a mi valor supone, mutatis mutandis, ya no sumar, sino multiplicar: x = x * r = 10 * ½ = 5. Si hubiera medido yo esa diferencia de perspectiva, habría obtenido r = 2, pero -para ponerme en los zapatos de mi hermana- comprendería que debo invertir la regla; en este caso, como la regla es multiplicativa, al invertirla la convierto en división: r = 1/r =  ½. Y, para comprobar que hemos invertido bien, lo que hacemos es multiplicar una regla por otra (r * r =  ½ * 2), de forma que el resultado no es ya 0 (que significa no sumar) sino 1 (que significa no multiplicar), pero está bien, pues de eso se trata, de quedarnos donde estábamos.

El siguiente paso consiste en hacer el caso multidimensional. Por ejemplo, imaginemos que el gato se ha subido a un árbol. En este caso, como no tengo una escalera que me lleve hasta el animal, utilizo dos pistas: mido mi distancia hasta el pie del árbol (x) y luego proyecto una línea perpendicular desde ese punto hasta el gato (y), componiendo así un triángulo rectángulo cuya base es x y cuya altura es y, lo cual me permite calcular la distancia a recorrer, mediante el Teorema de Pitágoras, como s = √(x² + y²). Por su parte, mi hermana comparte de nuevo mi origen, pero tiene otros ejes: ella se sirve de un terraplén que se eleva hacia el gato (digamos con un ángulo θ respecto del suelo), pero no lo alcanza, por lo que tiene que completar desde cierto punto (x) con un palo que se eleva en perpendicular desde el terraplén hasta el felino (y). Ella podría entonces medir directamente su x y su y, pero como siempre preferimos transformar mis valores.

Para ello, mi hermana debe medir la diferencia entre nuestras respectivas perspectivas, lo cual ahora se traduce en cuán inclinados están mis “metros” (a los que llamaré X e Y, con mayúscula) respecto de los suyos (que denomino también con mayúscula, X e Y). Este es un juicio que se hace por dimensiones. En efecto, lo de creerse uno el ombligo del mundo y el que tiene la rectitud es una tendencia tan fuerte que hasta la sufre cada una de nuestras personalidades.

El primer paso al frente lo da la cara X de mi hermana, que desea obtener la coordenada x. Lo primero que hace esta señora es medir mis dos perspectivas: observar las proyecciones de mis metros X e Y sobre ese eje X; obtiene así unas sombras, que están acortadas, las coordenadas cos θ y -sen θ.

Toca ahora aplicar esta regla a mis valores de la distancia hasta el gato, x e y. La dama X lo hace multiplicando cada oveja por su pareja (mi valor x lo multiplica por la forma en que ella lo ve, esto es, pasándolo por la lente que es cos θ; a mi y le aplica también el corrector correspondiente, que es  -sen θ) y luego suma esos productos. Como unos son positivos y otros negativos, el resultado es el efecto neto, que viene a ser la coordenada x, esto es, cuánto tiene la distancia hasta el gato de su eje X (el terraplén).

Para obtener la coordenada y, la faceta Y de mi hermana efectúa la misma operación: proyectar mis metros X e Y sobre su eje Y y obtener la diferencia de perspectiva con Y, esto es, las ratios sen θ y cos θ, y las emplea de la misma manera.

(Todo esto funciona así gracias, a que -tanto para mí como para mi hermana- los ejes y los metros X e Y son de valor unitario y perpendiculares entre sí, pero se hace algo largo de explicar y no quiero que los árboles no dejen ver el bosque.)

En conjunto, matemáticamente, esto se presenta como un producto entre matrices: a la derecha he puesto mis valores x e y para la distancia hasta el gato, que es lo que hay que transformar, como una matriz con una columna; a la izquierda vemos otra matriz (que llamo M) con dos columnas, una para mi unidad o perspectiva X y otra para la Y, pero medidas desde la perspectiva de mi hermana, por lo que me refiero a ellas con sus respectivos nombres (X e Y), aunque indicando en subíndice qué faceta de mi hermana las mide (X o Y). La gracia de multiplicar matrices es que se hace de la forma que avanzaba antes: la columna por cada línea (cada oveja con su pareja y sumando productos), lo cual permite pasar el vector de la derecha por el filtro de las perspectivas X e Y sucesivamente, como se ve aquí: 

Pero no hay que dejarse deslumbrar por el aparato técnico. Al fin y al cabo, estamos ante lo de siempre: se coge mi medición sobre la distancia hasta el gato y se le aplica lo que le falta para valer desde la perspectiva de mi hermana. Antes eso se traducía en añadir la distancia d, luego en aplicar la ratio r y ahora en multiplicar por la matriz M, pero nada más.

Para rematar, señalo que si yo hubiera medido la perspectiva de mi hermana, habría obtenido el mismo resultado que ella, pero organizado de otra forma. En concreto, habría obtenido una matriz con los mismos senos y cosenos del ángulo que nos separa, si bien mis columnas serían sus filas. Esto me valdría para transformar hacia mi perspectiva, pero si quiero “ponerme en su piel”, debería invertir esa matriz, lo que se consigue transponiéndola, esto es, cambiando las filas por columnas. La prueba de que esto es correcto es que si multiplico una matriz de transformación por la inversa el resultado es la matriz identidad, esto es, la que deja las cosas como están (la que si se aplica, no hace nada).

Llegamos así a la transformación de Fourier, cuyo aspecto aterrador era este:

Pero es fácil descubrir enseguida a nuestros viejos amigos, con un disfraz adaptado a las nuevas circunstancias. La principal novedad es que el problema a resolver es otro: nos encontramos ahora ante una señal que oscila alrededor de un punto de equilibrio (digamos por ejemplo el maullido del gato, que consiste en compresiones y estiramientos del aire con mayor o menor amplitud). Lo cómodo sería que este sonido tuviera un período que se repite, pero si no lo tiene, nos imaginamos que lo acaba teniendo en el límite, considerando un intervalo entre el menos infinito y el más infinito.

A la hora de medir la señal yo tomo la perspectiva de los instantes temporales: mido (con un osciloscopio) la amplitud del sonido en cada momento y lo represento como una función que toma como input cada instante y da como output una magnitud una amplitud del sonido. Esto es el f(x) que se ve en la ecuación y que se corresponde con el x de la distancia hasta el gato, en los dos primeros ejemplos, o el x e y del tercero; lo único que cambia es que ahora tengo una serie continua e infinita de valores, en vez de uno o dos.

Mi hermana toma por su parte la perspectiva de las frecuencias. Y es que en efecto cualquier sonido se puede ver como una suma de oscilaciones a distintas frecuencias, cada una con su amplitud correspondiente. Mi hermana podría utilizar un aparato (un espectrómetro) para obtener sus propios valores, pero como siempre preferimos transformar desde los míos.

A estos efectos, mi hermana debe proceder de nuevo a medir mi perspectiva desde la suya. Esto se traduce, como en el caso anterior, en que mide mis unidades (mis instantes), proyectándolas sobre las suyas (las frecuencias).

¿Cómo se come esto? Mutatis mutandis. Como ahora lo que medimos no es una distancia, sino una oscilación, no se mide con palos, sino -lógicamente- con osciladores. Concretamente, con un disco que rota, cuya representación es esta:

(Abajo en Anexo recuerdo por qué el número e, con este exponente, es un disco que rota)

Así pues mi hermana, si antes se situaba en su eje X y observaba la sombra que sobre él proyectaban mis metros X e Y, ahora lo que hace es ponerse en la rueda que gira a la frecuencia F y observar la sombra que sobre ella proyecta cada momento temporal T, esto es, anotar el lugar que ocupa el disco (lo que se llama la “fase”) en ese instante.

Acto seguido debe aplicar esta diferencia de perspectiva a mi medición de la señal f(x). Esto se traduce también en un producto de cada oveja con su pareja y suma de los resultados. Lo peculiar es que ahora los elementos son infinitos y continuos y por eso la suma de los productos es una integral. Para calcularla hay que evaluarla y esto requiere aplicar las técnicas del cálculo diferencial, pero tampoco hay que dejarse impresionar por estos términos, pues este cálculo es lo mismo que: en la versión más simple, coger el +10 y aplicarle un +d o un *r; en la multidimensional, coger cada uno de mis valores y multiplicarlos por un factor seno o coseno, a veces positivo y otras negativo, sacando al final el neto; de hecho ahora hacemos también esto mismo, con el matiz de que los resultados no miran simplemente a la derecha y a la izquierda, sino que apuntan en cualquier dirección y el neto lo sacaríamos (si es que pudiéramos hacerlo con infinitos elementos) mediante una suma vectorial, esto es, ligando todas las flechas (al extremo de una se junta la cola de otra) y trazando la raya que las une. El resultado será un número complejo que nos da la magnitud de la frecuencia y la dirección en la que apunta, su fase; con otras palabras, nos dice cuándo tiene que entrar cada frecuencia (cada nota) para acomodarse a la señal y en qué medida se acomoda.

Por fin, verán también un signo negativo en la fórmula, en el exponente. Para entender por qué conviene volver al ejemplo primero, el de la traslación. Allí todo se hacía sumando (es como se mide un objeto, cómo se mide la diferencia de perspectiva, cómo se aplica ésta…) y, por eso, para invertir la regla de conversión, para deshacer la suma, se restaba. Ahora lo que sucede en el exponente, la aplicación de las fases, también se traduce en una resta. Invertir es de nuevo cambiar el signo. Ahora bien, en qué transformación se pone el signo, en la de ida o la de vuelta, es una cuestión convencional y lo habitual es ponerla a la ida, como se refleja en nuestra fórmula.

Conclusión: he fracasado, quería explicar esto para niños y ni yo mismo lo entiendo, cuando lo intento leer al cabo de unos días, pero ¡que venga otro y lo perfeccione!

¿Y la conexión de esto con la muerte? Paciencia, ahora estoy muerto: ¡la próxima semana hablaremos de ello!

 Anexo: Por qué el nº e elevado a la i es un disco que rota

Como explicaba en otros posts, los números son adjetivos: cuentan una cualidad de las cosas, que es de cuántas unidades se componen. Pero son también adverbios, que nos dicen cómo hacer las operaciones con los números. Por ejemplo, yo puedo sumar 1 K, o sumarlo 2 veces (2K) o medio-sumarlo (1/2 K) o anti-sumarlo (-K). A esto, sumar conforme indica un coeficiente, lo llamamos multiplicar. Pero entonces la propia operación de multiplicar se puede efectuar de determinada manera, conforme indica un exponente. Por ejemplo, yo puedo multiplicar K por 2, o hacerlo 2 veces (K*2^2) o medio multiplicar por 2 (K*2^1/2 , que es raíz de 2)... Si multiplico el K por -1, tendré -K, es decir, habré girado mi K 180 grados; pero si lo medio-multiplico por -1, o sea, lo multiplico por raíz de -1... pues lo habré girado 1/4 de vuelta, 90 grados, lógicamente. De esta manera, lo que he hecho es mantener la magnitud del nº, pero darle una dirección totalmente independiente de la que tiene, una perpendicular a la original. A ese número que produce este efecto, raíz de -1, se le llama "i", la unidad "imaginaria", aunque se le podría haber denominado mejor la unidad perpendicular. 

Y ahora viene la gracia: ¿qué pasa si ahora este número i lo utilizo como adverbio? Por ejemplo, se lo pongo como exponente a un 2, como aquí 2^i, y entonces multiplico mi K "a la i", esto es, "a la perpendicular". Ojo: no lo estoy multiplicando por i, lo que tendría el efecto de girarlo un cuarto, sino por 2, pero "a la i". ¿Qué demonios es eso? Cuando multiplico una cosa por 2, la escalo dándole a cada una de esas unidades esa cualidad, pero en la misma dirección que ya tenía. Si ahora la multiplico por 2 "a la i", también la escalo, pero ya no para que crezca en su dirección originaria, sino para dotarle, también a cada una de sus unidades, de la dirección que en absoluto tiene, que es lo que significa perpendicular. Y darle a algo siempre dirección nueva es rotarlo, hacerle describir un círculo, que es lo que uno hace cuando está siempre cambiando de dirección.

El problema es cuánto arco se recorre. Para eso, hay que "normalizar", encontrar una unidad de escalado mediante rotación. La unidad de multiplicación longitudinal (de escalado en la misma dirección) es 2. La unidad de escalado mediante rotación es algo más, el nº e, que es  2,718 e infinitos decimales. De este modo, cuando se multiplica por e elevado a la i, resulta que se rota en arcos iguales al radio. O sea, si yo tengo un palo que mide K, pues al multiplicarlo por e^i lo roto en un arco igual a K, que es el radio de la circunferencia que K describe. Y como los ángulos de una circunferencia se pueden medir en arcos iguales a su radio o "radianes" (de los cuales la circunferencia tiene 2pi), habré rotado el K en un radian.

¿Por qué funciona así el número e? Se suele ejemplificar esto con el interés compuesto y continuo. Con un interés simple a tasa de 100% (esto es una velocidad de 1 K / año), lo doblamos, pero el nuevo capital lo dejamos aparte para sumarlo al final. Con un interés compuesto, seguimos doblando cada año, pero el nuevo capital no se aparta, sino que se acumula al antiguo, de forma que la 2º vez doblo 2, la 3ª 4 y así sucesivamente. Con un interés compuesto y continuo,  no esperamos al final de año para sumar el interés al capital, sino que se devenga y acumula en cada instante (ideal) del ejercicio (lógicamente por la parte proporcional), lo cual significa, a final de año, no doblar sino multiplicar por ese 2,718... (Para llegar a esta cifra se utilizan técnicas del cálculo diferencial, que aquí obviamos.)

Podemos decir así que la unidad de crecimiento de un interés simple es 1; la de un interés compuesto es 2 y la de un interés compuesto-continuo es 2,718... 

Si ahora cogemos esa unidad de interés compuesto continuo y le ponemos el exponente i, lo que sucede es curioso: el K rota, como manda el exponente i, y lo hace describiendo un arco a un tipo de interés del 100%, esto es, en una magnitud igual a su longitud, como si lo hubiéramos multiplicado por 2; ahora bien, ese efecto a lo largo del arco no se acumula y aumenta de forma compuesta y continua, sino que sigue la regla del interés simple, de forma que la próxima vez que multipliquemos por e^i lo que se volverá a doblar es el K inicial; ¿pero qué ha sido entonces de e y su efecto compuesto y continuo?; sucede que lo que actúa de forma compuesta (cada cambio de dirección opera sobre el acumulado anterior) y continua (en cada punto ideal) es solo el cambio de dirección. En suma, el ritmo de avance a lo largo del arco será siempre el K inicial multiplicado por el número que está en el exponente junto a i, es decir un cierto número de radianes; el resto del "efecto e" se consume en hacer que cambie la dirección de forma continua y compuesta.