Volver la vista atrás
Quiero
creer que el amable lector de este Blog se quedó en vilo al concluir la lectura
de la anterior entrada. Allí explicábamos que los números son adjetivos, aunque
todo el rato advertíamos de que empiezan siendo adverbios. ¿Y cómo es eso, se
habrá preguntado usted una y otra vez?
Para sacarle
por fin de su estado de intriga, retomaremos el ejemplo del monedero. Al
principio la bolsa contiene sólo una moneda de 1 €. Multiplicamos por 2 y le
imbuimos a nuestro capital “dosismo”, lo hacemos “dososo”. Luego lo
multiplicamos por 5 ¿y lo hacemos…? Aquí hay que tirar de la tabla que hemos
grabado en el disco duro de la memoria o, lo mismo da, en la calculadora de
mano. Se vuelve “diezoso”. ¿Por qué? Una posible respuesta es: “porque sí; si
quiere ser usted como nosotros, los expertos, tiene que habituarse a vivir en
los cielos de la abstracción, sin mirar jamás hacia abajo; y si no se lo cree,
le voy a contar otros cinco o seis conceptos de los más elevados y, como no los
va a entender, se quedará mudo y me dará la razón”. Lo mismo pasa en el ámbito
jurídico, con la pequeña diferencia de que ahí, con esta misma actitud, se puede
justificar una resolución o la contraria. ¿Por qué hay que condenar a “La
Manada” por abusos? Los jueces echaron
un vistazo a su particular tabla de multiplicar jurídica y leyeron: para que nos sintamos
“seguros”, mediante una aplicación restrictiva de los tipos penales. Y en la calle
se consultó otra tabla que conducía a lo opuesto: los acusados deben ser
condenados por violación porque es lo “justo”, ya que sabemos que forzaron a la
chica.
Sin
embargo, a uno u otro resultado (en Derecho) o al único resultado admisible (en
las ciencias exactas) se puede llegar también por una vía lenta, aunque más reveladora.
Centrándonos en el ejemplo matemático del monedero, en lugar de imaginar una
varita mágica que transforma la moneda de 1€ en un billete de 10€, podemos
visualizar una mano que entra y sale del monedero repetidas veces,
introduciendo cada vez una moneda de 1€.
Esta es la idea de que multiplicación es “adición repetida”, mucho más aburrida, menos aconsejable para razonar con prisas, pero reveladora de las tripas de la operación. Ah, pero cuidado: los expertos etiquetan esta explicación con la palabreja “MIRA” (Multiplication is Repeated Addition) y la critican, alegando que la idea sólo funciona en puridad para los números enteros positivos, pero empieza a padecer con el cero, los enteros negativos y las fracciones y rechina ya con los números irracionales (aquellos, como el número π, que no pueden ser generados por fracción alguna y tienen infinitos decimales, los cuales no siguen ningún patrón repetitivo…) Y si todavía tuvieran ustedes dudas al respecto -nos dicen los que saben- ¡a ver cómo se las arreglan para entender que un número ha sido sumado i veces, siendo i la unidad imaginaria, raíz cuadrada de -1…!
Esta es la idea de que multiplicación es “adición repetida”, mucho más aburrida, menos aconsejable para razonar con prisas, pero reveladora de las tripas de la operación. Ah, pero cuidado: los expertos etiquetan esta explicación con la palabreja “MIRA” (Multiplication is Repeated Addition) y la critican, alegando que la idea sólo funciona en puridad para los números enteros positivos, pero empieza a padecer con el cero, los enteros negativos y las fracciones y rechina ya con los números irracionales (aquellos, como el número π, que no pueden ser generados por fracción alguna y tienen infinitos decimales, los cuales no siguen ningún patrón repetitivo…) Y si todavía tuvieran ustedes dudas al respecto -nos dicen los que saben- ¡a ver cómo se las arreglan para entender que un número ha sido sumado i veces, siendo i la unidad imaginaria, raíz cuadrada de -1…!
Lo
reconozco. MIRA no lo explica todo. No siempre la multiplicación es adición efectuada
de forma repetida o reiterada. Pero es que el concepto bueno no es MIRA, sino otro
que suena muy cariñoso en español, MIMA (Multiplication
is Modified Addition). Y éste sí resuelve todo aquello. En efecto, cabe
juntar cosas de diversas maneras; dicho en términos gramaticales, el verbo
sumar admite una miríada de expresiones adverbiales. “Repetidas veces” es el
ejemplo señero, el más obvio. Pero caben otros “complementos circunstanciales”,
que cubren todos los casos indicados:
- Cuando el adverbio es cero, esto significa que “no se suma”.
- Si es un número negativo -n, se “anti-suma” (se resta) n veces.
- Si es ½, se “semi-suma” (se suma la mitad).
- Si es otra fracción, se “fraccio-suma” (se suma una parte).
- Si es un número irracional, se “fraccio-suma” también, si bien hay que hacerlo “de forma aproximada”: aquí por definición no hay fracción que abarque los infinitos decimales del número, pero podemos contentarnos con una que se aproxime a él en la medida apropiada (con el nivel de exactitud que demande cada situación práctica); por ejemplo, multiplicar por el número π se puede visualizar como sumar 3 veces o fraccio-sumar una décima parte (1/10) 31 veces o 314 veces una centésima (1/100) o 3.141 veces una milésima (1/1000)....
- Si por fin el adverbio es un número imaginario, confío en poder explicar más tarde cómo se “i-suma”.
[
Ojo, porque para que este planteamiento funcione hay que entenderlo así: si multiplicamos 1€ por 5, por ejemplo, hay que visualizar la mano que entra en el monedero 5 veces, sumando también ese 1€ inicial. Se siente la tentación de pensar: no, bueno, si se multiplica por n, lo que se hace es sumar (n-1) unidades a la unidad de partida. Pero eso no funcionaría a la hora de anti-sumar o restar: si se multiplica 1€ por -5, no se resta 4€ (esto daría 1 - 4 = -3), sino que se resta 1€ 5 veces, contando también el inicial.El siguiente cuadro sintetiza la idea:
(Advierto que la columna sombreada en amarillo utiliza una notación de mi invención, donde coloco el adverbio encima del signo de la operación para denotar que dicho signo es un adverbio que modifica la operación. Y también que K significa el objeto al que el número adjetiva o con el que se hacen operaciones en la forma que indica el número.)
Y en llegando aquí, debo mencionar ciertas objeciones que los expertos oponen al concepto de MIRA y probablemente opondrían también al de MIMA. Por ejemplo, ¿cómo se desmenuza en forma adverbial la combinación de dos unidades heterogéneas: un metro lineal en determinada dirección multiplicado por otro metro lineal perpendicular al anterior da un metro cuadrado; una unidad de masa por otra de aceleración da otra de fuerza...?
Esto lo resuelve la versión sintética o adjetival muy bien: estamos ante una multiplicación, porque adjetivamos un objeto; de hecho el objeto (por ejemplo, un palo de 1 metro) ya contaba con un adjetivo ("horizontal") y le añadimos otro ("vertical"), formando una unidad compleja, a la que bien podemos bautizar con un nuevo sustantivo ("1 metro cuadrado"). ¿Pero cómo juega la versión analítica o adverbial, cuál sería aquí la suma, efectuada de una u otra manera, en la que quepa descomponer la multiplicación?
Pues no lo voy a decir. No me da la gana. En una versión anterior de esta entrada, aventuré una explicación, pero la he quitado. A lo mejor pongo algo en el Apéndice, o en otra entrada futura. Pero no quiero contaminar ésta con tal discusión, porque lo que aquí digo es, en cambio, indiscutible. Lo que digo es que, en muchos casos, la multiplicación puede definirse volviendo la vista atrás, mediante un reverse engineering, como suma modificada. Y lo malo de no hacerlo sería que ese prejuicio nos haría perdernos lo mejor de la fiesta, de la fiesta de la abstracción: lo guay de ese conocimiento es que se puede tomar como inspiración cuando toca mirar hacia adelante y escalar la ladder of abstraction.
Volver la vista adelante
Así es, una vez que hemos aprendido a ver el número como un
adverbio que desvela cómo se han dado los pasos que componen una suma, hay que olvidarse de ese
rol y contemplarlo de nuevo como un adjetivo que sintetiza y codifica dichas
operaciones; hay que acuñar un verbo, multiplicar, que significa “atribuir uno de
esos adjetivos a una cosa”; y entonces la gracia consiste en repetir el
proceso, a partir de esta última plataforma: considerar que también el verbo
multiplicar (el oficio de atribuir cualidades) puede ser modificado mediante los
mismísimos adverbios que veníamos utilizando.
Tomemos los más elementales: 2, 0,
-1 y 1/2. Aplicados a la suma, significaban, respectivamente, sumar 2 veces, no
sumar, anti-sumar y semi-sumar. Ahora comprendemos que, aisladamente
considerados, significan operar 2 veces, no operar, anti-operar y semi-operar.
Por consiguiente, aplicados a la multiplicación, significarán multiplicar
varias veces, no multiplicar, anti-multiplicar y semi-multiplicar.
Naturalmente,
esta importación de sabiduría debe hacerse mutatis
mutandi, es decir, cambiando lo que haya que cambiar para adaptarse al
nuevo contexto. En nuestro caso:
Formalmente,
la diferencia es que, en sede de suma, el adverbio se suele colocar junto a la
cosa o grupo de cosas a sumar, normalmente delante, a modo de “coeficiente”; en
tanto que ahora, cuando el adverbio modifica una multiplicación, se sitúa como
un “exponente”, arriba y a la derecha del número por el que se multiplica (que
por esto se denomina la “base”). Por eso, a menudo se llama esta operación exponenciar,
lo que vendría a ser la versión sintética del verbo (la adverbial o analítica es
“multiplicación modificada”).
Materialmente,
en cuanto al significado de la operación, cambiará lo siguiente:
- Si el adverbio es un entero y se “multi-multiplica”, quiere esto decir que se va a atribuir una cualidad a un objeto repetidas veces, de forma sucesiva y por tanto acumulativa (el crecimiento exponencial es pues un crecimiento compuesto, donde cada nueva multiplicación opera sobre el resultado de la anterior).
- Si es cero, “no multiplicar” significa que no se atribuye al objeto ninguna cualidad, lo cual equivale a dejarlo como estaba, lo cual a su vez equivale a multiplicar por 1.
- Si es un número negativo, lo que procede es, en lugar de atribuir una cualidad a un objeto, quitársela (se “anti-multiplica” = se divide; por ejemplo, donde había un 4 = 2x2, dividir por 2 es quitar el adjetivo 2).
- Si es ½ , se “medio-multiplica”, se medio-asigna la cualidad que representa la base, lo cual significa multiplicar por la raíz cuadrada de la misma (o la raíz de índice m si el exponente es 1/m).
- Y si es un número irracional, como π, también se “aproxi-fraccio-multiplica”: como en la multi-suma, dependiendo del nivel de exactitud que se pretenda, trataremos a π como 3, como 31/10 o 314/100 o 3141/1000 y así por ejemplo, en este último caso, multiplicaríamos 3141 veces por una raíz (de la base, naturalmente) con índice 1000.
- Y si por fin el adverbio es la unidad de los números imaginarios (i), es verdad que uno se marea solo de pensar cómo puede “i-multiplicar”, esto es, atribuir la cualidad que representa la base, pero haciéndolo “a la raíz cuadrada de -1”. Esta es la típica cosa que, si fuera un salto y le pidieran a uno hacerlo, le daría miedo hacerlo mal y romperse la crisma…. Sin embargo, veremos pronto que es un salto sencillo.
En este cuadro resumo las distintas modalidades de "multiplicación modificada" y las coloco junto a las de "suma modificada", para que se aprecie bien cómo funciona la analogía:
(De nuevo advierto que las
columnas sombreadas en amarillo utilizan una notación de mi invención,
donde coloco el adverbio encima del signo de la operación para denotar que
aquel modifica esta última. Y también que K significa el objeto al que el número adjetiva o con el que se hacen operaciones en la forma que indica el número.)
Una visión financiera
Armados
con este conocimiento, podemos ponerlo en práctica con un ejemplo financiero,
el de un ahorrador que deposita un capital inicial (Ko) en un Banco. La
ventaja de este ejemplo es que nos conducirá, casi sin querer, a un nuevo
ascenso por la escalera de la abstracción.
Interés simple
Si nuestro
ahorrador vive aún en el primer peldaño de la escalera, sólo podrá optar a una
operación poco sofisticada, lo que podríamos llamar un crecimiento de su dinero
multi-sumativo o multiplicativo: el interés simple. Para consolarle, la entidad
financiera le ofrece una tasa de interés extraordinariamente generosa, del
100%. Esto significa que al final de cada año el Banco entrega al depositante
una copia exacta de su Ko. Si esto sucede a lo largo de t años,
diremos -en la versión adverbial o analítica- que hemos sumado al Ko
un clon del mismo (lo hemos doblado) una y otra vez y así hasta t veces, es
decir, que lo hemos “t-sumado”. Pero un spot publicitario, para lanzar un
mensaje más rápido e impactante, clamaría en versión adjetival: <<confíenos
su capital t años y le devolveremos lo invertido más un capital “t-oso”>>
o bien <<verá crecer su capital hasta devenir (1+t)-oso”. Lo cual en los
más austeros términos matemáticos se expresa así:
Kf = Ko + t Ko = (1 + t)
Ko
Supongamos
ahora que la entidad financiera, como era previsible, decide bajar la tasa,
pero sigue siendo magnánima y ofrece un 50%. En este caso, diremos: en la
versión adverbial, que anualmente al Ko no se suma, sino que
semi-suma un clon del mismo; en la adjetival, que el Ko deviene
“(1+medio-t)-oso”.
Generalizando,
para que la fórmula valga para cualquier tasa, podemos llamar a “r” a la
fracción en la que se concreta la tasa de interés (por ejemplo, 50%=50/100=1/2=0,5)
y la fórmula queda definitivamente así:
Kf = Ko + rt Ko
= (1 + rt) Ko
Adviértase
que, si el panorama financiero se complica, el Banco puede limitarse a
conservar el dinero, sin remunerarlo: en forma adverbial, “no suma”; en la
adjetival, da un interés “ceroso”. Y si la operación tiene riesgo, r será
negativo, en cuyo caso se “anti-suma” o al menos se “fraccio-anti-suma”… (¡y no
me obliguen a decir esto último con adjetivos!).
Interés compuesto
Ahora
bien, si el ahorrador es audaz y osa subir por la escalera de la abstracción,
podrá espetarle a su Banco: “oiga, esto de multi-sumar o multiplicar por t
el Ko es muy aburrido; ¿por
qué no me lo multi-multiplica o exponencia?” Lo que de esta forma pide el
depositante es que no se le pague interés simple, sino compuesto. Conforme a
este arreglo, cada año el interés no se extrae de la cuenta, sino que engrosa
el capital, participando así en la generación de interés en el siguiente período. De
este modo, si de nuevo partimos de la generosa tasa de interés del 100%, sucederá
que anualmente lo que se dobla no es el Ko, sino la inversión
acumulada hasta la fecha. La fórmula es ésta:
Kf
= 2t Ko
¿Y si en
lugar de pagar un 100% el Banco reduce el tipo? Me lanzo a consignar la fórmula
aplicable y la comento a continuación:
Kf = (1+r)t Ko
Es
importante destacar que la fracción r se halla en el piso de abajo, como
coeficiente, no en el de arriba, como exponente. A lo mejor esperaban ustedes
que dijera que, por efecto de un r < 1, se empieza a semi-multiplicar (con
una tasa del 50% = 50/100 = ½ = 0,5) o de otra manera fraccio-multiplicar. Eso
procedería, efectivamente, si r viviera en el ático: en ese caso al
semi-multiplicar (exponente = ½), multiplicaríamos por raíz cuadrada de la base;
o si el exponente fuera 1/3, multiplicaríamos por raíz cúbica de la base y así
sucesivamente. Pero no funciona así la fórmula del interés compuesto. Estamos
ante una exponenciación poco ambiciosa, porque sólo modifica la operación
inferior (la multiplicación) de la manera más obvia, haciéndola múltiple o
compuesta: como veíamos antes, lo que cada año se multiplica por una base no es
el capital inicial sino el acumulado, pero esta operación anual bien puede
verse como una suma o fraccio-suma (si se dobla la inversión acumulada porque
r=1, a la misma se le suma un clon completo; si r<1, se
fraccio-suma ese clon…).
Interés compuesto y continuo
Ahora bien, las cosas cambian cuando un
ahorrador ambicioso discurre así: sería ideal que me pagaran el interés con más
frecuencia que la anual (t*n), para que devengue antes capital y se ponga a
producir, digamos, cada trimestre (t*4) o cada mes (t*12) o cada día (t*365)…
Naturalmente, en ese caso el interés a abonar al final de cada período
infra-anual será proporcionalmente menor (r/n), pero incluso así la operación
puede ser ventajosa. En el extremo, podríamos calcular qué sucede cuando el
interés se paga cada instante, esto es, con una frecuencia que tiende a infinito.
La siguiente fórmula expresa esta idea:
Y aplicando
las técnicas del cálculo infinitesimal (véase el Apéndice), resulta que esto es
equivalente a (suponiendo un interés del 100%), en lugar de doblar la inversión
cada año, multiplicarla por el famoso número e, cuyo valor es 2,718 más una serie infinita de decimales. De este
modo la anterior fórmula se puede expresar de esta otra forma, mucho más
elegante:
Nótese que
ahora ya por fin la fracción r no habita en el piso bajo, a modo de coeficiente
(como en el interés compuesto ordinario), sino que ha ascendido a exponente y
la encontramos en el piso de arriba. Esto conlleva que, si queremos aplicar una
salomónica tasa del 50%, la inversión acumulada ya no se multiplicará por 1+ 1/2
= 1,5 de su valor, ni nada semejante, sino que se medio-multiplica por e, o sea, se multiplica por raíz cuadrada
de e = 1,648… Esto es muy importante.
En algún momento yo entendí qué significaba este cambio, pero se me estaba
olvidando. Me he tenido que ir a la cama pensando en ello y por la mañana me ha
vuelto la inspiración, afortunadamente, porque esto es la clave de bóveda del
edificio. La razón queda muy clara con nuestro modelo gramatical. El número e es un adjetivo que condensa, de modo
sintético, una serie de operaciones que conviene recordar: hemos tomado el Ko
y, dentro de cada período anual, lo hemos doblado (multiplicado por 1 + r
= 1 + 1 = 2) en un número de ocasiones tendente a infinito (n à ∞), si bien ajustando proporcionalmente la tasa (1/n).
¿Por qué elegimos esa tasa tan poco común (100%)? Bueno, alguna había que
elegir. Y al fin y al cabo el 2 que utilizamos al doblar es el estándar
natural, es la “unidad” de la multiplicación (la de la suma es 1, pero si
multiplicamos por 1 dejamos el resultado igual…). Así las cosas, cuando
queremos reintroducir una tasa más realista, no queda más remedio que hacerlo abarcando
todo ese sinfín de operaciones y la forma de hacerlo es empaquetando las mismas
en el adjetivo e y multiplicando por
el mismo “a la r”, con lo cual se logra que este adverbio (r) deje su huella en
todas las operaciones ocultas en las entrañas de e…
(Como prueba, cuando miren el Apéndice, verán que la demostración matemática de la fórmula, lo que en puridad dice, es esto mismo.)
(Como prueba, cuando miren el Apéndice, verán que la demostración matemática de la fórmula, lo que en puridad dice, es esto mismo.)
Por
consiguiente, casi sin darnos cuenta, hemos ascendido otro peldaño en la escalera
de la abstracción: hemos descubierto una nueva manera de multiplicar (la
continua), hemos conseguido codificarla en un adjetivo y bien podemos acuñar un
nuevo verbo para denotar el acto de atribuir a un objeto esa propiedad. Puesto
que el número e se suele denominar “número
de Euler”, podríamos llamar a este verbo de nuevo cuño “eulerizar”, en el bien entendido
de que (en forma analítica) significa multiplicar de forma compuesta y continua
a una tasa del 100% (r = 1) durante una unidad de tiempo (o las que indique su
exponente t).
Llegados a
este punto, estamos a un pasito de entender lo que se suele afirmar que es una
de las fórmulas más bellas de la matemática, la identidad de Euler, que tiene
este aspecto:
El reto es captar cómo se multiplica por e, cómo se "euleriza" (= se multiplica por 2, de modo compuesto y
continuo) “a la i” y "a la π". Lo veremos en la parte (IV) de esta serie.
APÉNDICE
Cómo se
obtiene en cálculo la fórmula del interés compuesto y continuo
El truco
es pensar en un número m cuyo valor fijamos en n/r.
Por tanto,
n = mr y podemos sustituir n en la fórmula por esta última expresión:
Si n tiende a infinito, también m tiende a infinito.
Y se sabe que la expresión en rojo con m tendente a infinito tiene su límite finito (converge) en el número e, con lo cual ya hemos concluido.
Pues bien, suele suceder que este tipo de demostraciones tan matemáticas, si lo piensa uno bien, debidamente traducidas al lenguaje natural, dicen una obviedad. En este caso, la misma que proponía arriba: que si queremos quitar la r del paréntesis, podemos hacerlo, pero entonces esto conduce a que la r desaparecida reaparezca como exponente, porque esto es la forma de obligar a que las operaciones que encierra dicho paréntesis se verifiquen "r-mente", esto es, que cuando multipliquemos por e lo hagamos fraccio-multiplicando en los términos que indique r.
Si n tiende a infinito, también m tiende a infinito.
Y se sabe que la expresión en rojo con m tendente a infinito tiene su límite finito (converge) en el número e, con lo cual ya hemos concluido.
Pues bien, suele suceder que este tipo de demostraciones tan matemáticas, si lo piensa uno bien, debidamente traducidas al lenguaje natural, dicen una obviedad. En este caso, la misma que proponía arriba: que si queremos quitar la r del paréntesis, podemos hacerlo, pero entonces esto conduce a que la r desaparecida reaparezca como exponente, porque esto es la forma de obligar a que las operaciones que encierra dicho paréntesis se verifiquen "r-mente", esto es, que cuando multipliquemos por e lo hagamos fraccio-multiplicando en los términos que indique r.




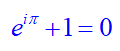
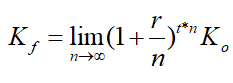

No hay comentarios:
Publicar un comentario